滤波反投影重建
要求
-
编程实现扇形束或平行束CT的滤波反投影重建算法,对前期通过解析计算或数值计算得到的Shepp Logan仿体投影数据进行重建;
-
将重建结果与原图进行比较,分析重建质量;
-
提交作业时,请简要描述思路,附上代码与结果(图像),以word或pdf形式提交。文件命名“4_FBP_学号_姓名.doc”
思路
使用图像旋转+像素累加得到的投影数据进行FBP重建。
1. 读取投影数据;
2. 构建R-L和S-L滤波器;
3. 编写重建算法函数,使用线性插值的方法计算图像每个像素点,遍历所有角度叠加的得到重建图像;
4. 分析重建图像质量;
结果
R-L和S-L滤波器
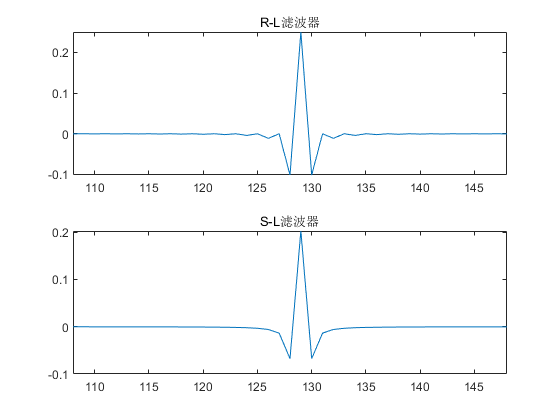
重建数值计算投影数据

从图像可以看出,使用不经过滤波器的投影数据直接重建,重建图像与原图有较大差异,出现明显信号失真。经过滤波器的两个重建图像与原始图像较为相似
比较重建结果
| PSNR | 直接反投影 | R-L滤波反投影 | S-L滤波反投影 |
|---|---|---|---|
| 原始图像 | 6.6571 | 17.2412 | 17.7826 |
| SSIM | 直接反投影 | R-L滤波反投影 | S-L滤波反投影 |
|---|---|---|---|
| 原始图像 | 0.1687 | 0.3487 | 0.3610 |
由结果可知,S-L滤波反投影的信噪比值最好,R-L滤波反投影的图像相似性较高。总而言之,经过滤波处理的重建图像较直接重建图像质量都有明显的提高。
代码
主程序
%% 初始化
clc,clear;
N = 256; % 图像大小
I = phantom(N); % Shepp-Logan头模型
theta = 0:1:179; % 投影角度
theta_num = length(theta);
d = 1; % 平移步长
delta = pi/180; % 角度增量
%% 读取投影数据
% P = radon(I,theta); % 生成投影数据
% [mm,nn] = size(P); % 计算投影数据矩阵的行、列长度
% e = floor((mm+1)/2);
% P1 = P(e-N/2:e+N/2-1,:); % 截取中心N点数据
a = load('Rdata.mat');
P1 = a.Rdata;
%% 构建滤波器
% 产生滤波函数
fh_RL = medfuncRlfilterfunction(N,d); % R-L滤波函数
fh_SL = medfuncSlfilterfunction(N,d); % S-L滤波函数
figure
subplot(2,1,1)
plot(fh_RL)
xlim([N/2-20,N/2+20])
title('R-L滤波器')
subplot(2,1,2)
plot(fh_SL)
xlim([N/2-20,N/2+20])
title('S-L滤波器')
% 直接反投影重建
rec = medfuncBackprojection(theta_num,N,P1,delta);
% R-L函数滤波反投影重建
rec_RL = medfuncfilteredbackprojection(theta_num,N,P1,delta,fh_RL);
%S-L函数滤波反投影重建
rec_SL = medfuncfilteredbackprojection(theta_num,N,P1,delta,fh_SL);
%% 图像展示
figure;
subplot(2,2,1),imshow(I),title('原始图像');
subplot(2,2,2),imshow(rec,[]),title('直接反投影重建图像');
subplot(2,2,3),imshow(rec_RL,[]),title('R-L函数滤波反投影重建图像');
subplot(2,2,4),imshow(rec_SL,[]),title('S-L函数滤波反投影重建图像');
a1 = psnr(funnormalization(I),funnormalization(rec));
a2 = ssim(funnormalization(I),funnormalization(rec));
b1 = psnr(funnormalization(I),funnormalization(rec_RL));
b2 = ssim(funnormalization(I),funnormalization(rec_RL));
函数
function fh_RL = medfuncRlfilterfunction(N,d)
% 生成RL滤波器
% 输入参数:
% N:图像大小,探测器通道个数
% d:平移步长
% 输出参数:
% fh_RL:R-L滤波函数
fh_RL = zeros(1,N);
for k1 = 1:N
fh_RL(k1) = -1/(pi*pi*((k1-N/2-1)*d)^2);
if mod(k1-N/2-1,2)==0
fh_RL(k1) = 0;
end
end
fh_RL(N/2+1) = 1/(4*d^2);
function fh_SL = medfuncSlfilterfunction(N,d)
% 生成SL滤波器
% 输入参数:
% N:图像大小,探测器通道个数
% d:平移步长
% 输出参数:
% fh_SL:S-L滤波函数
fh_SL = zeros(1,N);
for k1 = 1:N
fh_SL(k1) = -2/(pi^2*d^2*(4*(k1-N/2-1)^2-1));
end
function rec = medfuncBackprojection(theta_num,N,R1,delta)
% 不使用滤波器的重建算法
% 输入参数
% theta_num:投影角度个数
% N:图像大小
% R1:投影数据矩阵
% delta:角度增量(弧度)
% 输出参数:
% rec:反投影重建图像矩阵
rec = zeros(N); % 存储重建后的像素值
for m = 1:theta_num
pm = R1(:,m); % 取某一角度的投影数据
Cm = (N/2)*(1-cos((m-1)*delta)-sin((m-1)*delta));
for k1 = 1:N
for k2 = 1:N
% 以下为射束计算,射束编号n取值范围为1~N-1
Xrm = Cm+(k2-1)*cos((m-1)*delta)+(k1-1)*sin((m-1)*delta);
n = floor(Xrm); % 射束编号的整数部分
t = Xrm-floor(Xrm); % 射束编号的小数部分
n = max(1,n);n = min(n,N-1); % 限定n在1~N-1内
p = (1-t)*pm(n)+t*pm(n+1); % 线性内插
rec(N+1-k1,k2) = rec(N+1-k1,k2)+p; % 反投影,图像需旋转90°
end
end
end
function rec = medfuncfilteredbackprojection(theta_num,N,R1,delta,fh)
% 使用滤波器的重建算法
% 输入参数:
% theta_num:投影角度个数
% N:图像大小、探测器通道个数
% R1:投影数据矩阵
% delta:角度增量(弧度)
% fh:R-L滤波函数 S-L滤波器
% 输出参数:
% rec:反投影重建矩阵
rec = zeros(N);
for m = 1:theta_num
pm = R1(:,m);%某一角度的投影数据
pm_Ft = conv(fh,pm,'same');%做卷积
Cm = (N/2)*(1-cos((m-1)*delta)-sin((m-1)*delta));
for k1 = 1:N
for k2 = 1:N
%以下是射束计算,射束编号n取值范围为1~N-1
Xrm = Cm + (k2-1)*cos((m-1)*delta) + (k1-1)*sin((m-1)*delta);
n = floor(Xrm);%射束编号的整数部分
t = Xrm-floor(Xrm);%射束编号的小数部分
n = max(1,n);n = min(n,N-1);%限定n范围为1~N-1
p_RL = (1-t)*pm_Ft(n) + t*pm_Ft(n+1);%线性内插
rec(N+1-k1,k2) = rec(N+1-k1,k2)+p_RL;%反投影
end
end
end